國三的進度終於結束，之後的課程是複習測驗、測驗複習…檢討考卷時最常出現的畫面，就是學生為了要分數而一直與老師辯論…

這天～課堂上出現的小插曲也不例外，題目是這樣的：

『一棟高樓的陽台上，德元在10樓，德中在5樓，今取大小相同的兩鐵球標示甲、乙，德元拿甲球，德中拿乙球，兩球高度相差14.7公尺。令兩球同時自由落下，不計任何阻力，若甲球比乙球遲1秒鐘著地，則甲球原來的高度為  (A)19.6公尺  (B)29.4公尺 (C)39.2公尺 (D)44.1公尺』

看起來是很標準的自由落體計算。

改完之後檢討~學生提出意見：『這題答案應該是B，因為5樓與10樓高度差一半，所以是14.7公尺*2＝29.4公尺…』有道理，這題太簡單囉！！

『但，什麼？？答案不是B ！』原來這就是學生很堅持要分數的原因了。

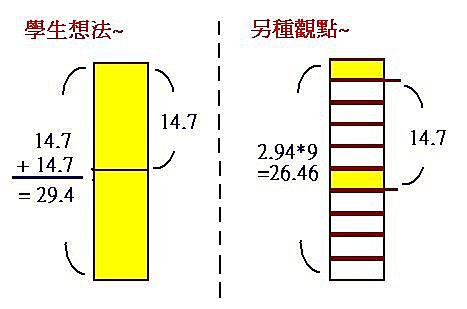
『那麼～是否可以這樣想： 5樓的陽台距地面事實上差4個樓高，10樓的陽台距地面差9個樓高，二者相距5個樓層，14.7公尺/5＝每個樓層是2.94公尺，，甲球在10樓，所以是9個樓高＝26.46公尺……但是，也沒這個答案！！

顯然這一題不能用樓高去推~『同一棟大樓～怎麼可能不是B？為什麼不能直接由樓高去算？？』

『也許有些樓是挑高樓中樓，有些則是違建，說不定德元他家五樓以上，是頂樓加蓋的違建！！』有這樣的說法~於是學生開始吵這題要送分了。

******

請出理化老師專業來幫忙～zfang老師很快看出這題的計算方法了，用標準的自由落體計算。

公式H=1/ 2gt² ，g=9.8，甲球的高度H甲=1/2×9.8(x+1)²  ，乙球的高度H乙=1/2×9.8(x)² 
H甲-H乙=14.7 去解x之值，最後得X=1，表示乙球在落地時間為1秒，而甲球的落地時間為2秒。將數據2秒帶入公式得到 H為19.6公尺  數字會說話~(A)是正解！

『但，什麼？？答案居然不是B ！』答案怎麼會是D?? 應該要修正。

『可是帶回公式算乙球的高度，卻只有4.9公尺。』學生也會有想法：『題目不是說～德中是在5樓嗎？怎麼可能距地面才4.9公尺而已？』

這是一個好問題！爭議題讓那一節課的討論氣氛到最高點。

既然答案出錯，題目也可能出錯，這種爭議題應該不至於出現在基測中~對學生說：『有時候不是理化本身觀念困難，而是國文程度的問題。』為了使得題目生活化，命題老師會多加入些文句，這些多加的文句常常產生讓作答者弄不清題意，或著是出題者的描述不夠清楚......，『這個題目其實是多了幾句，不必說德元、德中在幾樓就可以了～』以這題為例，反而使得題目變得矛盾。

如果出題老師是我，面對質疑可否硬拗呢？

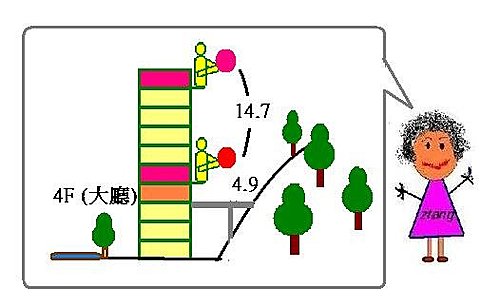
題目是問甲球原來的高度，並不是問10樓的樓高.....記得曾去過一些建在山坡地上的飯店，由大廳進入會發現自己所在的地方其實是四樓，如果房間在三樓，樓梯是要向下走的喔！

德元德中的所在的高樓~說不定就是蓋在山坡地上的飯店，而且做實驗的陽台是面對另一邊，落下的地面並非是一樓…是不是就合理多了呢這？？ （其實還是不要硬拗，承認錯誤並把題目修正才是正確的。）

要注意喔！萬一飯店是蓋在順向坡，還得小心有走山的危機呢！況且二兄弟違反安全，不可以為了自由落體實驗而隨意丟鐵球喔！

這個小小試題來找碴～讓昏昏欲睡的國三課堂樂了一下！

分類：教學現場與課堂側記 2010/04/30 15:20