[Jula] 開始．雜談．為什麼？ @新精讚

Julia 作為一個非常年輕的程式語言，至今大概3 4年而已(2018年起0.7, 1.0版釋出後，編譯器才趨於穩定)^[1]。

此篇是雜談，不是教學。

為什麼要去學習一個陌生的、全新的語言？

從開始學電腦程式，不知學習過多少語言，也不知放棄學習多少種語言。

隨著年紀增長，會越來越不想學習新的語言，畢竟所有語言都大同小異：

有的強調學習快、有的強調結構好、資源多、執行快或是平台擴展性，各有優缺點。

人能夠學習的範圍和時間很有限，語言只是一個工具，重點在於你要拿工具來做什麼？

所以重點千萬不要搞偏了。

回到主題，為什麼要去學習一個全新的語言，當然理由可以羅列幾十條，我覺得最要考慮的是學他能做什麼？

為什麼要學 JULIA？

關於Julia誔生的神話故事並不在我考慮的範圍，我得先看他的強項是什麼。

此文僅稍微整理一下，並把他的優缺點做個整理。

超強的線性代數能力

我覺得 julia很適合拿來算數學，尤其是線性代數

複數

利用 im 保留字輕鬆完成複數計算

julia> (1+3im)*(2+5im)
-13 + 11im
julia> (5-3im)^3
-10 - 198im

求項位角

利用angle並轉換成角度

julia> angle(1+2im)*180/pi
63.43494882292201

矩陣

下式等於是 $\left[ \begin{matrix} 1 \\2 \end{matrix} \right] \left[ \begin{matrix} 1 & 2 \end{matrix} \right]$

julia> [1;2;]*[1 2]
2×2 Matrix{Int64}:
1 2
2 4

反矩陣及轉置矩陣

其中 [1 2; 3 4] 代表矩陣 $\left[ \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} \right]$

julia> inv([1 2; 3 4;])
2×2 Matrix{Float64}:
-2.0 1.0
1.5 -0.5

共軛轉置

julia> ([1 2; 3 4;])'
2×2 adjoint(::Matrix{Int64}) with eltype Int64:
1 3
2 4

轉置矩陣及求值

julia> using LinearAlgebra <== 呼叫線代library
julia> A = [
           1 3 8
           2 -5 10
           -3 1 7
        ]
3×3 Matrix{Int64}: <== 定義結果
1   3   8
2 -5 10
-3   1   7
julia> transpose(A) <== 轉置矩陣
3×3 transpose(::Matrix{Int64}) with eltype Int64:
1   2 -3
3 -5   1
8 10   7

julia> det(A) <== 行列式求值
-281.0

安裝套件

安裝套件可以使用 Pkg函數

julia> using Pkg
julia> Pkg.add("Plots")

利用 Pkg的函數進行套件安裝，管理上方便

繪圖

julia> using Plots
julia> plot(rand(100,4), layout = 4, label=["a" "b" "c" "d"],
title=["A府" "B道" "C州" "D縣"], fontfamily="MingLiU" )

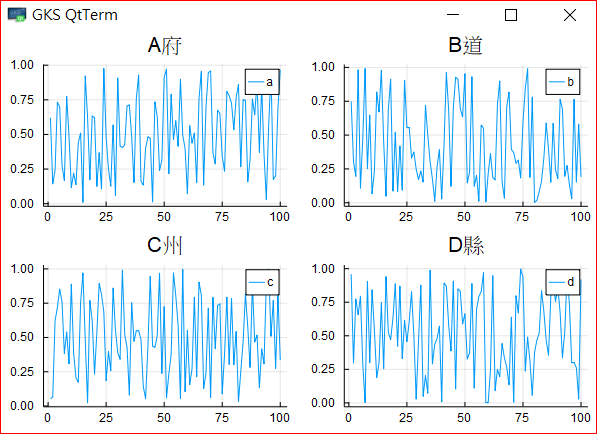
其它

分数

分数計算器

julia> 2//7+1//3
13//21

函數

julia> f(x) = 2x^3+x^2-5x-10
julia> g(x) = 2x-4
julia> h(x)= f(g(x))
julia> h(3)
0

集數合

求解集合數的和 $f (x) = \sum_{n = 0}^{∞} \frac{x^{n}}{n!}$

julia> f(x,nmax)= sum([x^n/factorial(BigInt(n)) for n=0:nmax])
julia> f(2,30)

7.389056098930650227230427182040632654314999242091465026550353896014737571231858

這是收斂函數，但其中 factorial()函數是算階乘，理論上在 20! 時就會溢位爆掉，但是透過 BigInt 還是可以算出值。

定積分

定積分有給定範圍的能夠計算，但如球體的體積分。

計算的精度就由切片的大小來決定，可以計算出定積分

<<程式撰寫中、待完成>>

多平台支援

Linux/ Windows/ Mac 等多平台多系統支援，同時也支援 ARM, IA64等架構

結論

優點

超強數學算力，很適合拿來做數學計算。

眾多使用者貢獻算力及各種方便的函數。

繪圖功能強大。

程式自由度高，對於類別和寫法寬容。

學習快速直覺。

缺點

因為輸入法干擾，交談環境有時游標會不見。

特殊符號在 linux上無法顯示。

線上文件仍有限，程式碼錯誤及說明提示不夠完備

總體而言，JULIA值得學習，尤其你需要做許多的數學物理方面的計算。

參考資料

[1] https://en.wikipedia.org/wiki/Julia_(programming_language)

[2] https://runebook.dev/ja/docs/julia/stdlib/linearalgebra/index#LinearAlgebra.det

[3] 小抄紙 https://juliadocs.github.io/Julia-Cheat-Sheet/

[4] https://docs.juliaplots.org/latest/generated/pyplot/

[5] http://park.itc.u-tokyo.ac.jp/kato-yusuke-lab/nagai/julianote.pdf