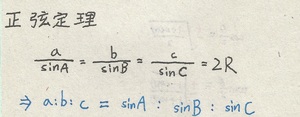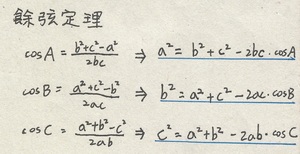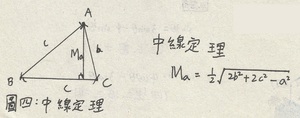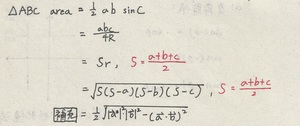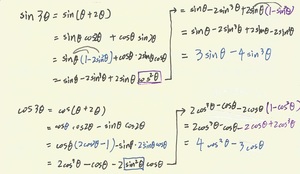Tips:點擊圖片可顯示原圖,字就不會糊糊的。
化為銳角之三角函數
下圖是所有三角函數之轉換,紅線畫開代表上下是不同的轉換,注意。
勘誤:第一點同界角裡sin(360+θ)應為sin(360n+θ),其餘兩個亦同
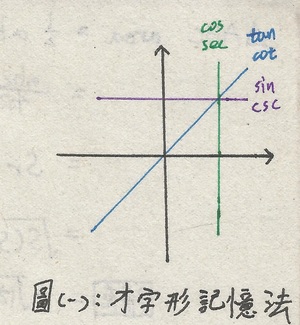
建議搭配下圖㈠才字形記憶法服用
其中,有被線經過的區域的三角函數值才為正,例如:sin的紫線經過了第一、二象限,所以sin在第一、二象限為正。
接著,就是沒有很好用的中線定理、正弦定理以及到高二下還是超好用的餘弦定理!
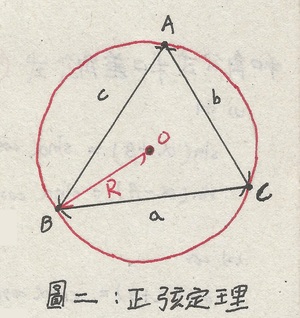
其中代號各是代表什麼請參考下圖㈡
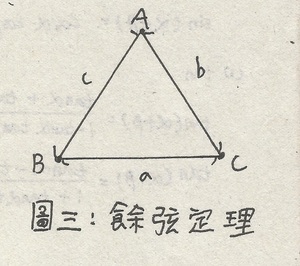
緊接而來的是餘弦定理!
餘弦定理有兩種形式的寫法,可以挑一種覺得好記的來記,兩種各有優缺點,箭頭左邊算cos值較快,右邊則算邊長較快;而那些代號又是什麼意思呢?參考下圖㈢
再來就是小編使用率不高的中線定理
因為中線定理不長,所以就和圖㈣放在一起
三角形面積公式
P.S.area為面積的英文
紅筆的地方要特別注意,還有R表示外接圓半徑,r則是表示內切圓半徑,而最下面是向量的算法,就當補充順便列出
第四個等號那條公式又稱海龍公式
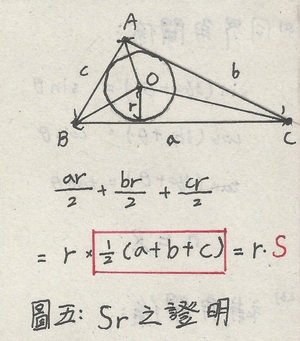
若想知道三角形面積為什麼會等於Sr可以參考下圖㈤
和角公式和差角公式
這真的只能用背的,後面的倍角公式和半角公式都是由這裡下去做推導,所以,這裡沒背後面一定就不會
倍角公式
然後是三倍角的
紫色掛號裡是背誦口訣,但是下面那句要用台語念,所以小編特別將羅馬拼音用鉛筆標上去
一樣,推導過程如下圖所示:
上半部是sin3θ的推導過程,下半部則是cos3θ的推導過程。
半倍角公式
最後最後,就是半倍角,這個結束就沒了。
※正負號一定要記得
順帶一提,小編也只有背二倍和三倍角公式,半倍角公式長得真的太醜了,每次小編要用都自己用推導的把他推出來,小編推導的過程如下: