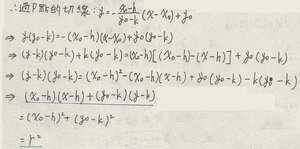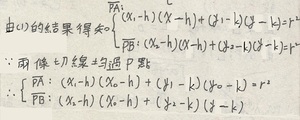設圓C:x2 + y2 + dx + ey + f = 0或(x - h)2 + (y - k)2 = r2
P點座標(x0, y0)
|
怎麼分一半: x2 = x · x —其中一個x用x0代入→ x0 · x y2 = y · y —其中一個y用y0代入→ y0 · y x = (x+x)÷2 —其中一個x用x0帶入→ (x+x0)÷2 y = (y+y)÷2 —其中一個y用y0帶入→ (y+y0)÷2 因為沒有未知數,所以常數項不變 |
將P點代入圓C可得下列兩條分一半公式:
x · x0 + y · y0 + d(x · x0)÷2 + e(y · y0)÷2 + f = 0
或
(x - h)(x0 - h)+ (y - k)(y0 - k) = r2
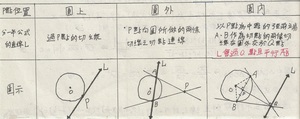
使用分一半公式所得出來的結果是一條二元一次方程式,其幾何意義依P點位置區分如下表:
證明pf>
⑴ P在圓上
∵過P點的切線會⊥線段OP
∴切線斜率 = -(1 ÷ mop) = -[(x0 - h)÷(y0 - k)]
⑵P在圓外
設P點向一圓所做的兩條切線之切點為A(x1 , y1)、B(x2 , y2) 兩點
∴A(x1 ,y1)、B(x2 , y2)均滿足方程式(x - h)(x0 - h)+ (y - k)(y0 - k) = r2
且兩點可決定一直線,故直線AB的方程式為(x0 - h)(x - h) + (y0 - k)(y - k) = r2
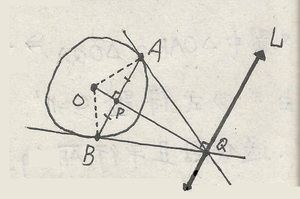
⑶P在圓內
如圖 ∵P為弦AB的中點
∴線段AB⊥線段OP