熟悉的一直是家中到學校的街景，這天，決定在市區亂亂『騎』~意外地在東興路上看到一間奇妙的建築物，『呀~玻璃屋，好像碳60球體！』

過幾天，在課堂上對學生提到起我的發現。『那間我去過，就在我家附近，』翔文說：『裡面賣衣服，還有一個大樓梯可以到二樓，它以前是賣咖啡的……』決定利用午休專程去拍照。原先還以為是預售屋，玻璃屋夾雜在一些建築物間，其實不算太顯眼，如果它的週遭是綠地或是白色建築，會更美~

走進門口看到鐵架，哦~原來是這樣搭建的。其實，它是由許多三角形玻璃窗所組合，，而且並非完全相同的等腰或正三角形；它的最頂端是由五片玻璃組成的五邊形，其他周圍則是六邊形，它，接近球體，但與碳60不同！

『妳看~』我手指著上方的幾何形狀：『有些是五邊形有些是六邊形，而且這些三角形並不規則。』
『原本沒注意這麼多，』她點點頭：『最近要加貼隔熱紙，請人來估價時，也注意到這點。』

經過銷售小姐請示經理許可，讓我在室內走動觀察拍照。這間採光很好，室內也佈置得很舒適，時值中午，幸好冷氣夠強，否則像溫室，鐵定會熱吧！『老師~下次再來，順便看一下我們的衣服！』ㄟ~這個嘛...再說啦~

國二上到有機單元，又在自然領域研習中看到碳60的模型，恰巧與我看到的玻璃屋，共同做個小文章整理一下。

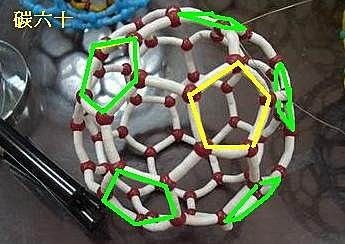
碳60、碳70其實是由五邊形與六邊形組合而成，結構要穩定，要有12個五個五邊形，上下六個(1個為頂~5個為輔)。以多面體結構來說，碳60為切角20面體，由60個碳原子組成，60個頂點，90個邊（60×3÷2＝90，註）。共有32個面（12個五角形和20個六角形），我的算法：
(1)考慮共用點 60×3＝180 (每個點被三個形狀共用)
(2)要組成一個封閉的球，上下要有12個五角形；12個五角形用去12×5＝60個點
(3)180－60＝120個頂點；120÷6＝20 (20個六角形)
註：若用化學角度，計算鍵結形式，每一個碳原子，與相鄰的三個碳原子鍵結，90個邊，其中30個C＝C雙鍵(由1個δ鍵及1個π鍵組成)，60個C－C單鍵 (δ鍵)。每一個C以sp2混成軌域彼此鍵結形成單鍵，且均剩下一個pz電子，而每一個π鍵需2個pz電子，60個C有60個pz電子，故可形成30個π鍵。單鍵數目：90－30＝60。

******

12個正五邊形，不僅能和20個六邊形構成C60，還可以和其他數目的六邊形組成蛋形的多面體，例如碳70。多年前曾在教甄中考過計算C60、C70的邊、面 (還包括五角形六角形數目)與鍵數，當時的我不會…現在這樣算，不知對不對？

我的參考計算：
碳70，70 個頂點，每個碳接3個，70×3÷2＝105個邊，70pz÷2= 35個雙鍵，105-35＝70個單鍵。
70個點 × 3＝210；210－60＝150 (12個五角形用去60個點)；150÷6＝25 (六邊形) ；共12個五邊形，25個六邊形。
如果想看切角20面體，碳60碳70與奈米碳管相關資料，最容易被搜尋到的資料便是國家高速網路與計算中心，張自恭博士 http://nano.nchc.org.tw/dictionary/c60.html

至於科博館大門的多面體，則是12個頂點，20 面體（均為三角形）。

原文發表於2008/04/21