『想想~三面鏡子其中之一夾角為45°的萬花筒，得到的圖案會是什麼形呢? 』

『45度的四面鏡子如何做成萬花筒? 我百思不得其解，尚祈指教哦~』王德麟(Darling Wang)老師曾在流轉的圖案~萬花筒如此回應。45度，四面鏡子~我真的這樣寫。哇，出現錯誤了~趕快修正，否則不只百思不解，萬思也難解。

為了詳細解說，外加展現zfang回覆的誠意，我把翔翔咬一角的萬花筒拆了，裡面不是玻璃，只是發亮的三片金屬片，就以這三片作為小實驗吧。

首先，拆去『小碎花』反向往觀察孔看去，形成6個小圓孔，如果恰巧有人往此處看，我們或看到許多『小眼睛』(感覺有些恐怖)。

接著，解釋一下成像的簡單計算，一般萬花筒是利用正三角形，每個夾角上面的『小碎花』，經過多次反射，形成五個像，連同本身，組成六邊形。

以夾角90度的二面鏡子為例，物體分別與鏡，形成像1、像2，再次反射形成像3。物與像1、像2等距，垂直平分~以O’為圓心，物距為半徑做一圓，物與像皆在圓上。

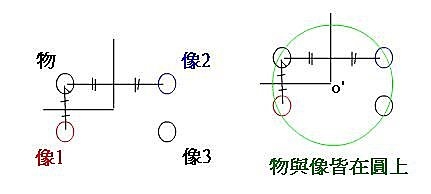
360 ÷ 90 = 4 (連同原物，共四個圖案，形成四邊形)
360 ÷ q = n ，取整數，形成n邊形

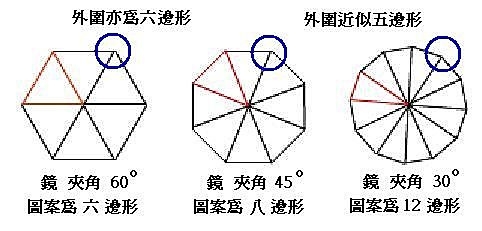
針對不同角度進行計算，正三角形的三面鏡子，每一個角皆是形成6邊形的圖案。如果是45度角，360 ÷ 45 = 8，圖案為八邊形，但另二個角度為67.5，360 ÷ 67.5 = 5.3，取整數為扭曲五邊形。
夾角如果更小(例如30度)，圖案的重複性會更大，形成12邊形(快接近圓形了)。而另外二的角，360 ÷ 75 = 4.8，四邊形(?)。

>

然後~可以做實驗了......以等腰三角形作為基本形狀，調整二金屬片角度。

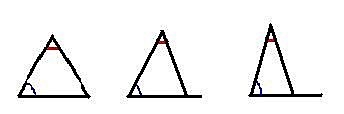
『三面鏡子其中之一夾角為45°的萬花筒，得到的圖案會是什麼形呢?』(答案反白可見~一個八邊形的圖案，與另外二個五邊形的圖案。 )

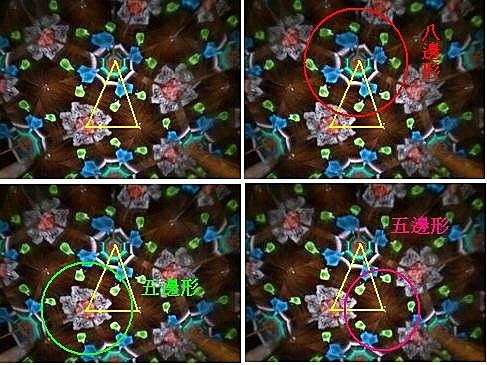
眼花撩亂了吧~

最後~猜一猜，下列萬花筒圖案，其中二面鏡的夾角幾度？

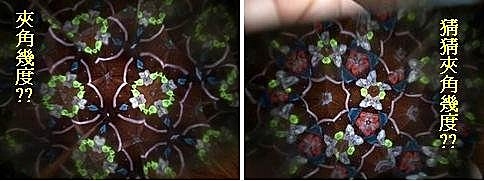
(答案反白後可見：左圖，45度；右圖，40度，9邊形)

哇~花了快四個小時終於完成這篇~(其實每一篇文章都花好多功)，回覆的這篇文章...夠誠意吧！

原文發表於2008/03/26